Managing MySQL at Serverless Scale

"What? You can't use MySQL with serverless functions, you'll just exhaust all the connections as soon as it starts to scale! And what about zombie connections? Lambda doesn't clean those up for you, meaning you'll potentially have hundreds of sleeping threads blocking new connections and throwing errors. It can't be done!"  ~ Naysayer

I really like DynamoDB and BigTable (even Cosmos DB is pretty cool), and for most of my serverless applications, they would be my first choice as a datastore. But I still have a love for relational databases, especially MySQL. It had always been my goto choice, perfect for building normalized data structures, enforcing declarative constants, providing referential integrity, and enabling ACID-compliant transactions. Plus the elegance of SQL (structured query language) makes organizing, retrieving and updating your data drop dead simple.

But now we have SERVERLESS. And Serverless functions (like AWS Lambda, Google Cloud Functions, and Azure Functions) scale almost infinitely by creating separate instances for each concurrent user. This is a MAJOR PROBLEM for RDBS solutions like MySQL, because available connections can be quickly maxed out by concurrent functions competing for access. Reusing database connections doesn't help, and even the release of Aurora Serverless doesn't solve the max_connections problem. Sure there are some tricks we can use to mitigate the problem, but ultimately, using MySQL with serverless is a massive headache.

Well, maybe not anymore. 😀 I've been dealing with MySQL scaling issues and serverless functions for years now, and I've finally incorporated all of my learning into a simple, easy to use NPM module that (I hope) will solve your Serverless MySQL problems.

Introducing Serverless MySQL

Serverless MySQL is a wrapper for Doug Wilson's amazing mysql Node.js module. It adds a connection management component to the mysql module that is designed specifically for use with serverless applications. The module can monitor the number of connections being utilized, and then based on your settings, manage those connections to allow thousands of concurrent executions to share them. It will reuse connections when possible, clean up zombie threads, enforce connection limits per user, and retry connections using trusted backoff algorithms.

In addition, Serverless MySQL also adds modern async/await support to the mysql module, eliminating callback hell or the need to wrap calls in promises. It also dramatically simplifies transactions, giving you a simple and consistent pattern to handle common workflows.

NOTE: This module has been tested with AWS's RDS MySQL, Aurora MySQL, and Aurora Serverless, but it should work with any standards-based MySQL server.

A Simple Example

javascriptCopy code
// Require and initialize outside of your main handler
const mysql = require('serverless-mysql')({
  config: {
    host     : process.env.ENDPOINT,
    database : process.env.DATABASE,
    user     : process.env.USERNAME,
    password : process.env.PASSWORD
  }
})

// Main handler function
exports.handler = async (event, context) => {
  // Run your query
  let results = await mysql.query('SELECT * FROM table')

  // Run clean up function
  await mysql.end()

  // Return the results
  return results
}

Installation and Requirements

Serverless MySQL is an NPM module that can be installed and included in your Node.js functions.

defaultCopy code
> npm i serverless-mysql

This module uses modern JavaScript methods and therefore requires Node 8.10+. It also requires the use of a MySQL-compatable server/cluster.

There really isn't anything special that needs to be done in order for your MySQL server (including RDS, Aurora, and Aurora Serverless) to use serverless-mysql. You should just be aware of the following two scenarios.

If you set max user_connections, the module will only manage connections for that user. This is useful if you have multiple clients connecting to the same MySQL server (or cluster) and you want to make sure your serverless app doesn't use all of the available connections.

If you're not setting max user_connections, the user MUST BE granted the PROCESS privilege in order to count other connections. Otherwise it will assume that its connections are the only ones being used. Granting PROCESS is fairly safe as it is a read only permission and doesn't expose any sensitive data.

How to use Serverless MySQL 🚀

Serverless MySQL wraps the mysql module, so it supports pretty much everything that the mysql module does. It uses all the same connection options, provides a query() method that accepts the same arguments when performing queries (except the callback of course), and passes back the query results exactly as the mysql module returns them. There are a few things that don't make sense in serverless environments, like streaming rows, so there is no support for that yet.

To use Serverless MySQL, require it OUTSIDE your main function handler. This will allow for connection reuse between executions. The module must be initialized before its methods are available.

There are a number of supported configuration options (including event callbacks) detailed in the documentation. These must be passed in during initialization.

javascriptCopy code
// Require and initialize with default options
const mysql = require('serverless-mysql')() // <-- initialize with function call

// OR include configuration options
const mysql = require('serverless-mysql')({
  backoff: 'decorrelated',
  base: 5,
  cap: 200
})

MySQL connection options can be passed in at initialization (using the config property) or later using the config() method.

javascriptCopy code
mysql.config({
  host     : process.env.ENDPOINT,
  database : process.env.DATABASE,
  user     : process.env.USERNAME,
  password : process.env.PASSWORD
})

You can explicitly establish a connection using the connect() method if you want to, though it isn't necessary. This method returns a promise, so you'll need to await the response or wrap it in a promise chain.

javascriptCopy code
await mysql.connect()

Running queries is super simple using the query() method. It supports all query options supported by the mysql module, but returns a promise instead of using the standard callbacks. You either need to await them or wrap them in a promise chain.

javascriptCopy code
// Simple query
let results = await query('SELECT * FROM table')

// Query with placeholder values
let results = await query('SELECT * FROM table WHERE name = ?', ['serverless'])

// Query with advanced options
let results = await query({
  sql: 'SELECT * FROM table WHERE name = ?',
  timeout: 10000,
  values: ['serverless'])
})

Once you've run all your queries and your serverless function is ready to return data, call the end() method to perform connection management tasks. This will do things like check the current number of connections, clean up zombies, or even disconnect if there are too many connections being used. Be sure to await its result before continuing.

javascriptCopy code
// Perform connection management tasks
await mysql.end()

Note that end() will NOT necessarily terminate the connection. Only if it has to in order to free up connections. If you'd like to explicitly terminate connections, use the quit() method instead.

javascriptCopy code
// Gracefully terminate the connection
mysql.quit()

If you need access to the connection object, you can use the getClient() method. This will allow you to use any supported feature of the mysql module directly.

javascriptCopy code
// Get the connection object
let connection = mysql.getClient()

// Use it to escape a value
let value = connection.escape('Some value to be escaped')

Transaction Support 🙌

Transaction support in Serverless MySQL has been dramatically simplified. Start a new transaction using the transaction() method, and then chain queries using the query() method. The query() method supports all standard query options.

You can specify an optional rollback() method in the chain. This will receive the error object if a transaction fails, allowing you to add additional logging or perform some other action. Call the commit() method when you are ready to execute the queries.

javascriptCopy code
let results = await mysql.transaction()
  .query('INSERT INTO table (x) VALUES(?)', [1])
  .query('UPDATE table SET x = 1 ')
  .query('SELECT * FROM table')
  .rollback(e => { /* do something with the error */ }) // optional
  .commit() // execute the queries

Automatic Connection Retries and Backoff 🤓

Serverless MySQL will automatically kill idle connections or disconnect the current connection if the connUtilization limit is reached. Even with this aggressive strategy, it is possible that multiple functions will be competing for the same available connections. The backoff setting uses the strategy outlined here to use Jitter instead of Exponential Backoff when attempting connection retries.

The two supported methods are full and decorrelated Jitter. Both are effective in reducing server strain and minimize retries. The module defaults to full.

Full Jitter: LESS work, MORE time

javascriptCopy code
sleep = random_between(0, min(cap, base * 2 ** attempts))

Decorrelated Jitter: MORE work, LESS time

javascriptCopy code
sleep = min(cap, random_between(base, sleep * 3))

You can also provide your own backoff algorithm.

Does this thing actually work? 🤔

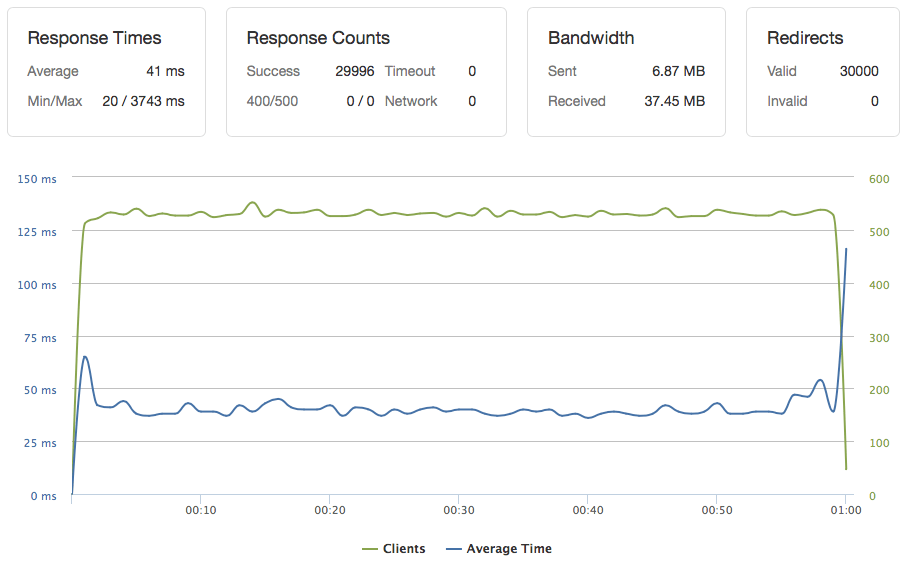
Fair question. I've run a lot of tests using a number of different configurations. Ramp ups appear to work best, but once there are several warm containers, the response times are much better. Below is an example test I ran using AWS Lambda and Aurora Serverless. Aurora Serverless was configured with 2 ACUs (and it did not autoscale), so there were only 90 connections available to the MySQL cluster. The Lambda function was configured with 1,024 MB of memory. This test simulated 500 users per second for one minute. Each user ran a sample query retrieving a few rows from a table.

From the graph below, you can see that the average response time was 41 ms (min 20 ms, max 3743 ms) with ZERO errors.

Other tests that use larger configurations were extremely successful too, but I'd appreciate other independent tests to verify my assumptions. 📊

Where do we go from here?

There is plenty more to do with this module. I've done a number of simulated tests, but there are several others that need to be run. The module also needs some automated tests written along with code coverage reporting. I'll be adding that soon so that we don't introduce regressions as new features are added.

I've actually been using this module in production for quite some time and it has worked perfectly for several of my applications. Even if you are not experiencing massive scale, this module is a handy tool for simply managing your connections and providing a more intuitive interface into the mysql module.

I'd love to know your thoughts and see your test results. There is always room for improvement, so your feedback, bug reports, suggestions, and contributions are greatly appreciated.

Good luck! 🤘🏻